こんにちは。キリンコ先生です!
今回から、実際に問題を解いてもらって、必要な考え方などを解説していこうと考えていますので、お付き合いのほどよろしくお願いします。
それではこの問題を解いてみてください。
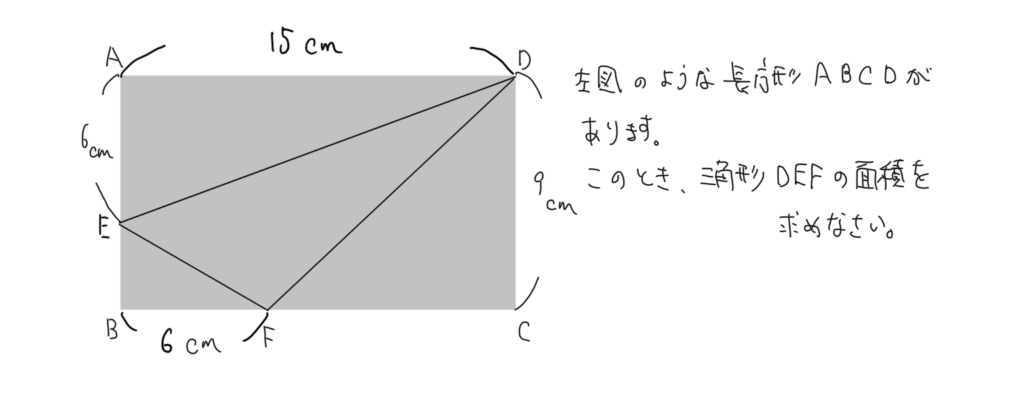
みなさん解けましたか?
この問題は、長方形の面積と三角形の面積の求め方を知っているお子様であれば、全員解くことができます。この問題を3つの解法で解説していきたいと思います。
①全体から引く
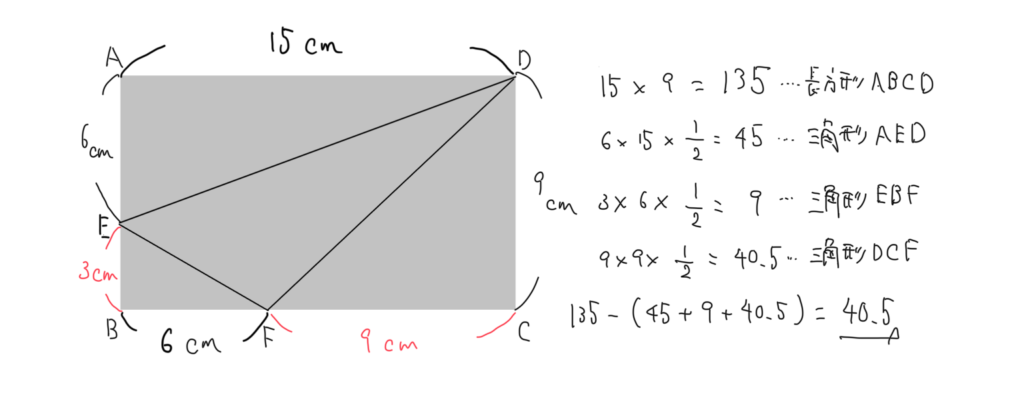
この方法で解いた人が多いと思います。この全体から引くという考え方は面積を求めるときだけではなく、場合の数などでも使う重要な考え方です。まずはこの方法で必ず出せるようになりましょう。
次の解法は、受験を考えている小学生、中学生のどちらの人も身につけたい考え方です。
②面積を直接求める
この解法に必要な考え方があるので、まずはこれを見てください。
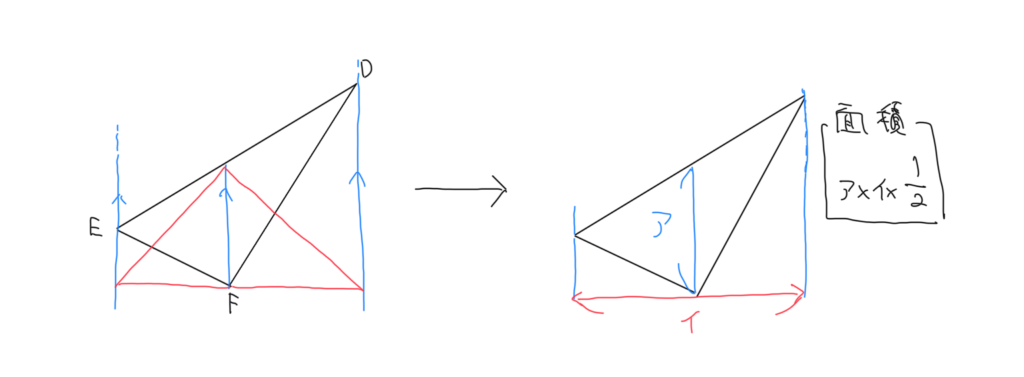
平行な線の間に挟まれている三角形の面積は、底辺の長さを変えなければ、形を変えても面積が変わらないという等積変形という考え方があります。この考え方を使うと、三角形DEFは赤い三角形に変形しても面積は変わらないことになります。赤い三角形は右図のアが高さで、イが底辺と考えられるので、結局、三角形DEFの面積は右図のように出せることになります。
この三角形のような形の処理の仕方を習得しましょう。小学生はこのような形が平面図形の問題で出てきて、中学生は関数の問題で出てきます。
これを使うとこんな感じで解けます。
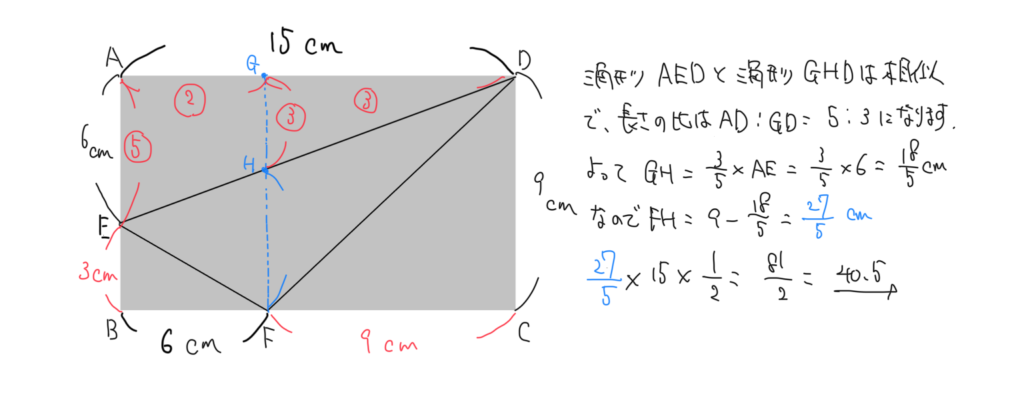
この問題では相似という考え方を使わないとFHが出せません。なので相似をまだ習っていない人はFHの長さが分かってからのやり方を身につけましょう!
最後の解法は1次関数を習っている人たち限定の考え方です。
③座標平面上で考える
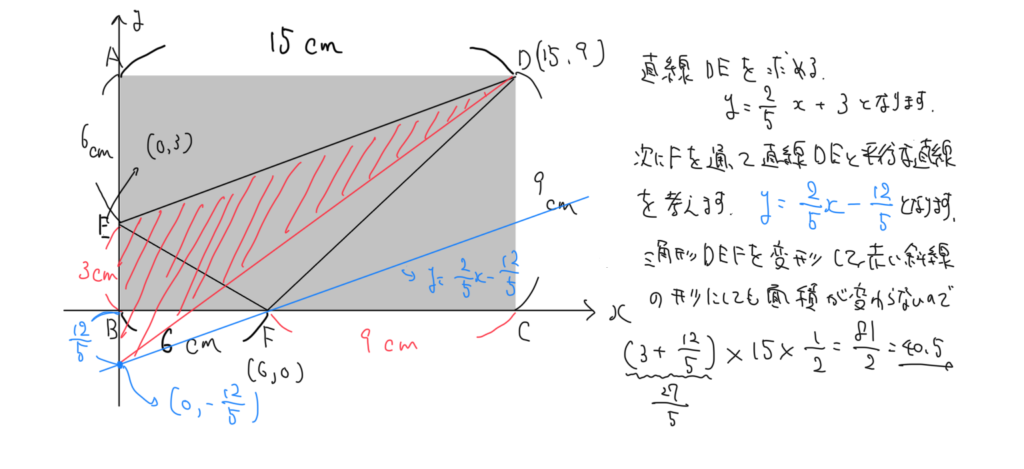
こんな形で与えられている図形をそのまま座標平面上で扱うと、直線の式を出したりすることができるようになるので、処理の仕方を変えることができます。
あとは先ほども紹介した等積変形の考え方で形を変えて解いていくといった流れです。
算数・数学はこんな形で、答えは一つでもアプローチがたくさんあるところが面白いポイントです!
そして、たくさんの解法を知っておくことは、前にも話した通り見直しにもつながります。
なので問題が解けたら終わりではなく、この方法ではダメなのかな、など1つの問題で色々なことを試してみるのが試行錯誤にもなり、とても良いでしょう!
ではまた次回もよろしくお願いします!

